정점(데이터)끼리의 연결관계를 저장한 자료형
[용어정리]
<기본>
- 정점 : 연결의 대상이 되는 개체
- 간선 : 개체 사이의 연결
<그래프의 종류>
- 무방향 그래프(양방향 가능)
- 방향 그래프
- 가중치 그래프
- 완전 그래프 : 각각의 정점에서 다른 모든 정점을 연결한 그래프
- 부분 그래프 : 원 그래프의 일부 정점 및 간선으로 이워진 그래프
<집합 표현법>
- 그래프 G의 정점 집합 V(G)={A, B, C, D}
- 그래프 G의 간선 집합 E(G)={(A,B), <A,C>} (* ()는 무방향, <>는 방향 그래프)
[그래프의 두가지 구현방법]
- 인접 행렬 기반 그래프 (두 정점이 연결되어 있으면 1, 연결되어 있지 않으면 0으로 표시)
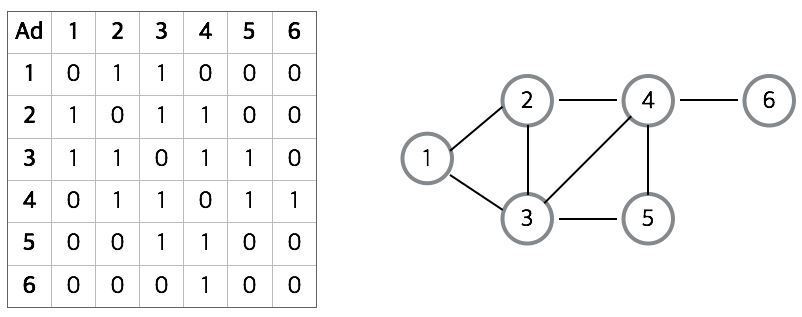
- 인접 리스트 기반 그래프
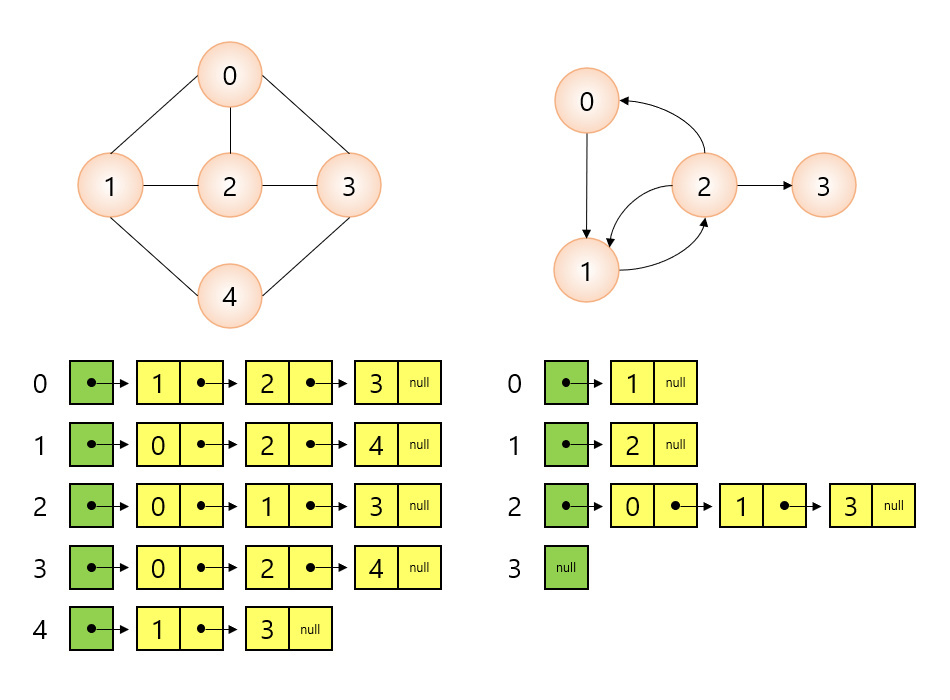
▶ 그래프의 ADT
필요한 기능 : 그래프 초기화, 그래프 리소스 해제(그래프 자체 없엠), 연결된 간선 추가, 모든 정점의 간선 정보 출력
void GraphInit(ALGraph * pg, int nv); // 그래프의 초기화
void GraphDestroy(ALGraph * pg); // 그래프의 리소스 해제
void AddEdge(ALGraph * pg, int fromV, int toV); // 간선의 추가
void ShowGraphEdgeInfo(ALGraph * pg);
<특징>
- 초기화와 동시에 정점의 수를 결정
- 간선을 추가는 하되 삭제는 불가능하도록 정의함
[인접 리스트 기반의 그래프 구현]
▶ 구현
- 그래프를 의미하는 구조체
typedef struct _ual
{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
} ALGraph;
- ADT의 구현
// 그래프의 초기화
void GraphInit(ALGraph * pg, int nv)
{
int i;
pg->adjList = (List*)malloc(sizeof(List)*nv);
pg->numV = nv;
pg->numE = 0; // 초기의 간선 수는 0개
for(i=0; i<nv; i++)
{
ListInit(&(pg->adjList[i])); //리스트 초기화
SetSortRule(&(pg->adjList[i]), WhoIsPrecede);
}
}
// 그래프 리소스의 해제
void GraphDestroy(ALGraph * pg)
{
if(pg->adjList != NULL)
free(pg->adjList);
}
// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE += 1;
}
// 모든 정점의 간선정보 출력
void ShowGraphEdgeInfo(ALGraph * pg)
{
int i;
int vx;
for(i=0; i<pg->numV; i++)
{
printf("%c와 연결된 정점: ", i + 65);
if(LFirst(&(pg->adjList[i]), &vx))
{
printf("%c ", vx + 65);
while(LNext(&(pg->adjList[i]), &vx))
printf("%c ", vx + 65);
}
printf("\n");
}
}
int WhoIsPrecede(int data1, int data2)
{
if(data1 < data2)
return 0;
else
return 1;
}
<특징>
- void GraphDestroy(ALGraph * pg) -> 그래프의 간선을 지우는게 아니라 그래프 자체를 없에 버리는 함수임
- void AddEdge(ALGraph * pg, int fromV, int toV) -> 무방향 그래프는 양방향으로 간선을 추가하므로 LInsert 2번 호출함
'자료구조' 카테고리의 다른 글
| [자료구조] 해쉬(Hash)와 테이블(Table) (0) | 2022.05.02 |
|---|---|
| [자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) (0) | 2022.04.24 |
| [자료구조] 트리(Tree) (0) | 2022.04.17 |
| [자료구조] 덱(Deque) (0) | 2022.04.10 |
| [자료구조] 큐(Queue) (0) | 2022.04.10 |
정점(데이터)끼리의 연결관계를 저장한 자료형
[용어정리]
<기본>
- 정점 : 연결의 대상이 되는 개체
- 간선 : 개체 사이의 연결
<그래프의 종류>
- 무방향 그래프(양방향 가능)
- 방향 그래프
- 가중치 그래프
- 완전 그래프 : 각각의 정점에서 다른 모든 정점을 연결한 그래프
- 부분 그래프 : 원 그래프의 일부 정점 및 간선으로 이워진 그래프
<집합 표현법>
- 그래프 G의 정점 집합 V(G)={A, B, C, D}
- 그래프 G의 간선 집합 E(G)={(A,B), <A,C>} (* ()는 무방향, <>는 방향 그래프)
[그래프의 두가지 구현방법]
- 인접 행렬 기반 그래프 (두 정점이 연결되어 있으면 1, 연결되어 있지 않으면 0으로 표시)

- 인접 리스트 기반 그래프

▶ 그래프의 ADT
필요한 기능 : 그래프 초기화, 그래프 리소스 해제(그래프 자체 없엠), 연결된 간선 추가, 모든 정점의 간선 정보 출력
void GraphInit(ALGraph * pg, int nv); // 그래프의 초기화
void GraphDestroy(ALGraph * pg); // 그래프의 리소스 해제
void AddEdge(ALGraph * pg, int fromV, int toV); // 간선의 추가
void ShowGraphEdgeInfo(ALGraph * pg);
<특징>
- 초기화와 동시에 정점의 수를 결정
- 간선을 추가는 하되 삭제는 불가능하도록 정의함
[인접 리스트 기반의 그래프 구현]
▶ 구현
- 그래프를 의미하는 구조체
typedef struct _ual
{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
} ALGraph;
- ADT의 구현
// 그래프의 초기화
void GraphInit(ALGraph * pg, int nv)
{
int i;
pg->adjList = (List*)malloc(sizeof(List)*nv);
pg->numV = nv;
pg->numE = 0; // 초기의 간선 수는 0개
for(i=0; i<nv; i++)
{
ListInit(&(pg->adjList[i])); //리스트 초기화
SetSortRule(&(pg->adjList[i]), WhoIsPrecede);
}
}
// 그래프 리소스의 해제
void GraphDestroy(ALGraph * pg)
{
if(pg->adjList != NULL)
free(pg->adjList);
}
// 간선의 추가
void AddEdge(ALGraph * pg, int fromV, int toV)
{
LInsert(&(pg->adjList[fromV]), toV);
LInsert(&(pg->adjList[toV]), fromV);
pg->numE += 1;
}
// 모든 정점의 간선정보 출력
void ShowGraphEdgeInfo(ALGraph * pg)
{
int i;
int vx;
for(i=0; i<pg->numV; i++)
{
printf("%c와 연결된 정점: ", i + 65);
if(LFirst(&(pg->adjList[i]), &vx))
{
printf("%c ", vx + 65);
while(LNext(&(pg->adjList[i]), &vx))
printf("%c ", vx + 65);
}
printf("\n");
}
}
int WhoIsPrecede(int data1, int data2)
{
if(data1 < data2)
return 0;
else
return 1;
}
<특징>
- void GraphDestroy(ALGraph * pg) -> 그래프의 간선을 지우는게 아니라 그래프 자체를 없에 버리는 함수임
- void AddEdge(ALGraph * pg, int fromV, int toV) -> 무방향 그래프는 양방향으로 간선을 추가하므로 LInsert 2번 호출함
'자료구조' 카테고리의 다른 글
| [자료구조] 해쉬(Hash)와 테이블(Table) (0) | 2022.05.02 |
|---|---|
| [자료구조] 우선순위 큐(Priority Queue)와 힙(Heap) (0) | 2022.04.24 |
| [자료구조] 트리(Tree) (0) | 2022.04.17 |
| [자료구조] 덱(Deque) (0) | 2022.04.10 |
| [자료구조] 큐(Queue) (0) | 2022.04.10 |
