[알고리즘] PS에 필요한 수학지식
<목차>
- 나머지 연산
- 최대공약수 / 최소공배수 (유클리드 호제법)
- 소수 (에라토스테네스의 체)
- 팩토리얼에서 0의 갯수 구하기(소인수분해)
- 조합에서 0의 갯수 구하기(소인수분해)
▶ 나머지 연산
<덧셈>
(A + B) % M = (A%M + B%M) % M
<곱셈>
(A * B) % M = (A%M * B%M) % M
<뺄셈> : 뺄셈의 경우 A%M - B%M가 음수가 나올수도 있으므로 M을 더해준다
(A - B) % M = (A%M - B%M + M) % M
<나눗셈> : 성립하지 않는다 !
▶ 최대공약수(GCD) / 최소공배수(LCM)
최대공약수 : A, B 두 수의 공통된 약수중에 가장 큰 수
최소공배수 : 두 수의 공통된 배수 중에 가장 작은 정수
⊙ 최대공약수 구하기
<노가다 방식>
int g = 1;
for (int i=2; i<=min(a,b); i++)
{
if (a % i == 0 && b % i == 0)
{
g = i; // 공약수중에 가장 큰 수가 g에 저장된다
}
}
<유클리드 호제법 이용> - 유도식은 알면 다쳐
유클리드 호제법이란 : GCD(a, b) = GCD(b, a%b) ,,,, 쭉 계산하다가 a%b가 0 이면 그때의 b가 최대공약수다
ex) GCD(24, 16) = GCD(16, 8) = GCD(8, 0) = 8
- 재귀함수로 유클리드 호제법 구현
int GCD(int a, int b)
{
if (b == 0) // b가 0이 될때까지 함수 반복
{
return a;
}
else
{
return GCD(b, a%b);
}
}
- for문을 이용한 유클리드 호제법 구현
int GCD(int a, int b)
{
while(b == 0)
{
int r = a%b;
a=b;
b=r;
}
return a;
}
⊙ 최소공배수 구하기
최소공배수 구하는 법 : 최소공배수 * 최대공약수 = A * B 이므로 이를 이용한다
최소공배수= (A * B) / 최대공약수가 되겠지?
▶ 소수 구하기
⊙ 소수 : 약수가 1과 자기 자신 밖에 없는 수
⊙ 소수관련 알고리즘
- 어떤 수 N이 소수 인지 아닌지 판별
- 1부터 N까지 범위 안에 들어가는 모든 소수를 구하는 법
⊙ 어떤 수 N이 소수 인지 아닌지 판별 (시간 복잡도 : O(루트N))
bool Prime (int num)
{
if(num<2)
{
return false;
}
for(int i=2; i*i < num; i++) // i = 루트(num)까지만 판별해도 소수인지 아닌지 나옴
{
if(num % i == 0)
return false;
}
return true;
}
⊙ 1부터 N까지 범위 안에 들어가는 모든 소수를 구하는 법 = 에라토스테네스의 체 (★)
시간복잡도 : O(NloglogN)
이론 :
- 2부터 N까지의 모든 수를 써놓는다
- 아직 지워지지 않은 수중에 가장 작은 수를 찾는다
- 그 수는 소수이다
- 이제 그 수의 배수를 모두 지운다
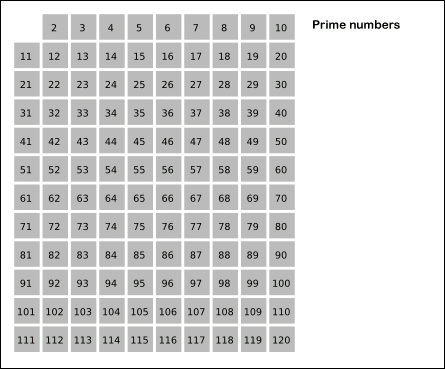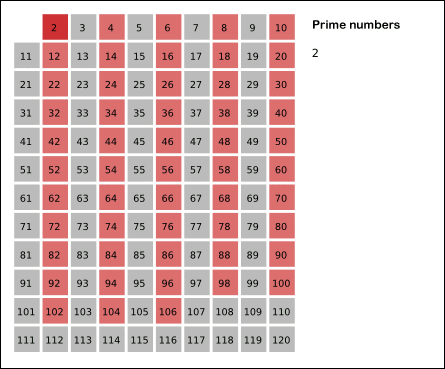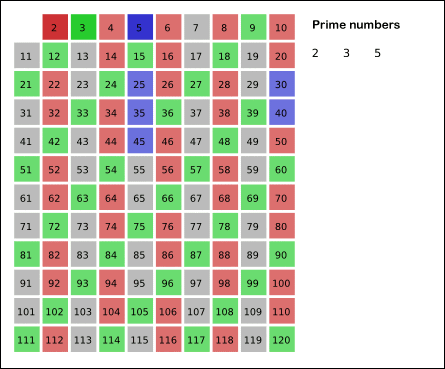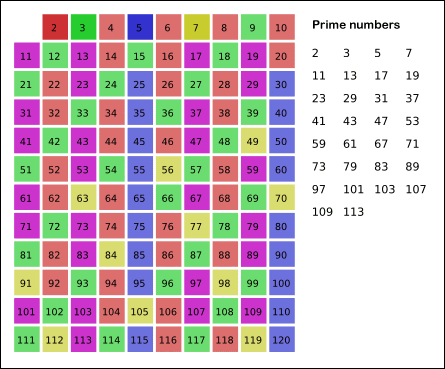
※ 3 * 2 는 2가 이미 지웠으므로 지울 필요가 없다 (3* 3 부터 지우면 됨)
--> 11 * 11은 121로 120을 넘기 때문에 더이상 수행할 필요가 없음
코드 :
int prime[120]; // 소수 저장
bool check[120]; // 소수면 false 저장, default값 : false
int pnum = 0; // 소수의 갯수
int n = 120; // n=120
for(int i=2; i<n; i++)
{
if(check[i] == false)
{
prime[pnum] = i;
pnum++;
for(int j= i*2; j<=n; j+=i)
{
check[j]=true;
}
}
}
▶ 팩토리얼에서 0의 갯수 구하기
0의 갯수를 구하는 방법은 소인수분해(2와 5의 갯수)를 해보면 알수 있다
팩토리얼에선 5의 갯수 < 2의 갯수 이므로,,, 소인수분해 결과의 5의 갯수 = 0의 갯수가 된다
ex) 100!의 경우 1~100에서 인수로 5가 들어가는 것을 찾으면 됨 5*1, 5*2, 5*3, 5*4, 5*5,,,,
--> 여기서 5*5는 5가 2번 들어가니까 인수로 한번 더 세줌
▶ 조합에서 0의 갯수 구하기
0의 갯수를 구하는 방법은 소인수분해(2와 5의 갯수)를 해보면 알수 있다
조합에선 2의 갯수가 많을지 5의 갯수가 많을지 모름으로,,,2의 갯수 vs 5의 갯수 중 적은것이 조합에서 0의 갯수가 된다